一、BF算法和RK算法：

举例：两个字符串：主串： a b b c e f g模式串： b c e

第一轮，我们从主串的首位开始，把主串和模式串的字符逐个比较：

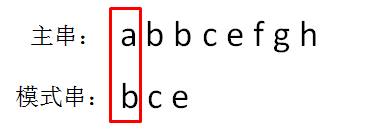
显然，主串的首位字符是a，模式串的首位字符是b，两者并不匹配。第二轮，我们把模式串后移一位，从主串的第二位开始，把主串和模式串的字符逐个比较：

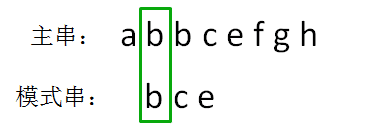
主串的第二位字符是b，模式串的第二位字符也是b，两者匹配，继续比较：主串的第三位字符是b，模式串的第三位字符也是c，两者并不匹配。

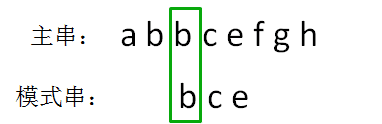
第三轮，我们把模式串再次后移一位，从主串的第三位开始，把主串和模式串的字符逐个比较：主串的第三位字符是b，模式串的第三位字符也是b，两者匹配，继续比较：主串的第四位字符是c，模式串的第四位字符也是c，两者匹配，继续比较：主串的第五位字符是e，模式串的第五位字符也是e，两者匹配，比较完成！

由此得到结果，模式串 bce 是主串 abbcefgh 的子串，在主串第一次出现的位置下标是 2：这就是BF算法（暴力算法）。

但是，这种算法在某些极端情况下效率很低，例如字符串aabbbbbbbbsbd和子串bd匹配。

假设主串的长度是m，模式串的长度是n，那么在这种极端情况下，BF算法的最坏时间复杂度是O（mn）。

BF算法的改进（RK算法）：

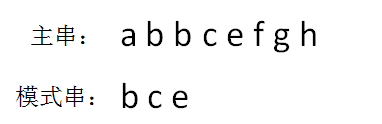
给定主串和模式串如下（假定字符串只包含26个小写字母）：第一步我们需要生成模式串的hashcode。生成hashcode的算法多种多样。

按位相加

这是最简单的方法，我们可以把a当做1，b当做2，c当做3…然后把字符串的所有字符相加，相加结果就是它的hashcode。bce = 2 + 3 + 5 = 10但是，这个算法虽然简单，却很可能产生hash冲突，比如bce、bec、cbe的hashcode是一样的。使用按位相加计算hash值，需要对相同的hash值的两个字符串进行一对一比较，若相同就是匹配成功，若是不能一一对应，则代表匹配失败。

转换成26进制数

既然字符串只包含26个小写字母，那么我们可以把每一个字符串当成一个26进制数来计算。bce = 2*(26^2) + 3*26 + 5 = 1435这样做的好处是大幅减少了hash冲突，缺点是计算量较大，而且有可能出现超出整型范围的情况，需要对计算结果进行取模。为了方便演示，这里我们采用的是按位相加的hash算法，所以bce的hashcode是10：

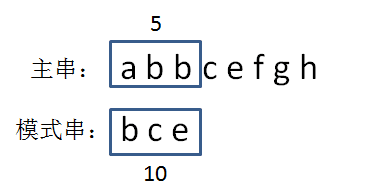
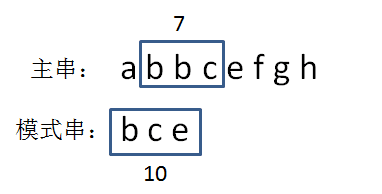
第二步生成主串当中与模式串第一个相同长度的等长子串的hashcode。（由于主串通常要长于模式串，把整个主串转化成hashcode是没有意义的，只有比较主串当中和模式串等长的子串才有意义）因此，我们首先生成主串中第一个和模式串等长的子串hashcode，即abb = 1 + 2 + 2 = 5：接着在进行比较，显然5！=10，继续下一轮的比较。第三步，生成主串当中第二个等长子串的hashcode。bbc = 2 + 2 + 3 = 7：接着在进行比较，显然7！=10，继续下一轮的比较。第四步，生成主串当中第三个等长子串的hashcode。

bce= 2 + 3 + 5 = 10：接着进行比较，显然10 ==10，两个hash值相等！这是否说明两个字符串也相等呢？

由于存在hash冲突的可能，我们还需要进一步验证。

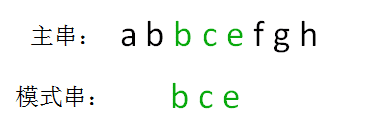
第五步，逐个字符比较两字符串。hashcode的比较只是初步验证，之后我们还需要像BF算法那样，对两个字符串逐个字符比较，最终判断出两个字符串匹配。最后得出结论，模式串bce是主串abbcefgh的子串，第一次出现的下标是2。

对哈希值计算的优化，每次计算子串的哈希值，不需要逐个相加，可以在原来子串哈希值的基础上减去第一个字符的哈希值再加上最后一个字符的哈希值来得到最新的哈希值。比如：这两个子串的哈希值如何求，我们可以主要解决：新hashcode = 旧hashcode - 1 + 4 = 26-1+4 = 29同理，接下来的其他子串都可以这样求。

下面给出算法的代码实现：

public class 字符串匹配 { public static int strKarp(String str,String pattern) { int m=str.length(); int n=pattern.length(); int patternCode=hash(pattern); int strCode=hash(str.substring(0, n)); for(int i=0;i

BM算法：

坏字符规则：

坏字符：指模式串和子串当中不匹配的字符。还以上面的字符串为例，当模式串和主串的第一个等长子串比较时，子串的最后一个字符T就是坏字符：BM算法的检测顺序：从字符串的最右侧向左开始检测。因为只有模式串与坏字符T对齐的位置也是字符T的情况下，两者才有匹配的可能。不难发现，模式串的第1位字符也是T，这样一来我们就可以对模式串做一次“乾坤大挪移”，直接把模式串当中的字符T和主串的坏字符对齐，进行下一轮的比较：坏字符的位置越靠右，下一轮模式串的挪动跨度就可能越长，节省的比较次数也就越多。这就是BM算法从右向左检测的好处。接下来，我们继续逐个字符比较，发现右侧的G、C、G都是一致的，但主串当中的字符A，是又一个坏字符：我们按照刚才的方式，找到模式串的第2位字符也是A，于是我们把模式串的字符A和主串中的坏字符对齐，进行下一轮比较：接下来，我们继续逐个字符比较，这次发现全部字符都是匹配的，比较公正完成。

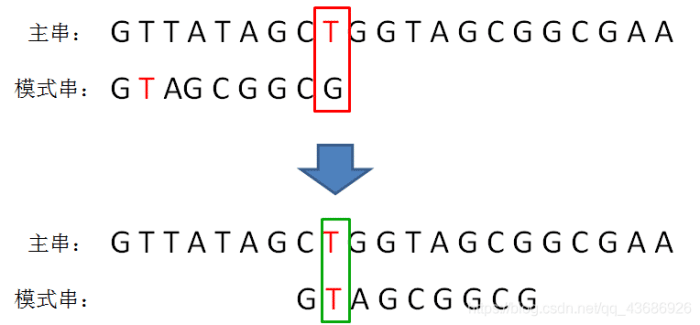
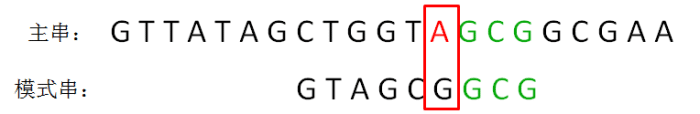
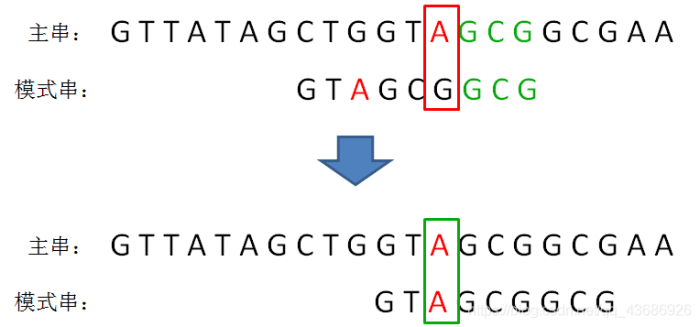
坏字符的规则代码编写：

public class 字符串匹配的坏字符规则 { public static int bM(String str,String pattern) { int sl=str.length(); int pl=pattern.length(); int start=0; while(start <= sl-pl) { int i;for(i = pl-1; i >= 0; i--) { if(str.charAt(start+i) != pattern.charAt(i)) { break; } if(i<0) {return start; } int charIndex=findChar(pattern,str.charAt(start+i),i); int off=charIndex>=0 ? i-charIndex : i+1; start += off; } } return -1; } private static int findChar(String pattern, char charAt, int index) { for(int i=index-1;i>=0;i--) {if(pattern.charAt(i) == charAt) { return i; } } return -1; } public static void main(String[] args) { String str="GBTTTATAGCTGGTAAGCGBGCGATA"; String pattern="GTAAGCG"; int index=bM(str, pattern); System.out.println("首次出现的位置是："+index); }}

总结：字符串匹配各种算法的核心思想是：利用模式串中某个字符与主串不能匹配的时候，将模式串往后多滑动几位，以此来减少不必要的字符比较，提高匹配的效率。

分享到